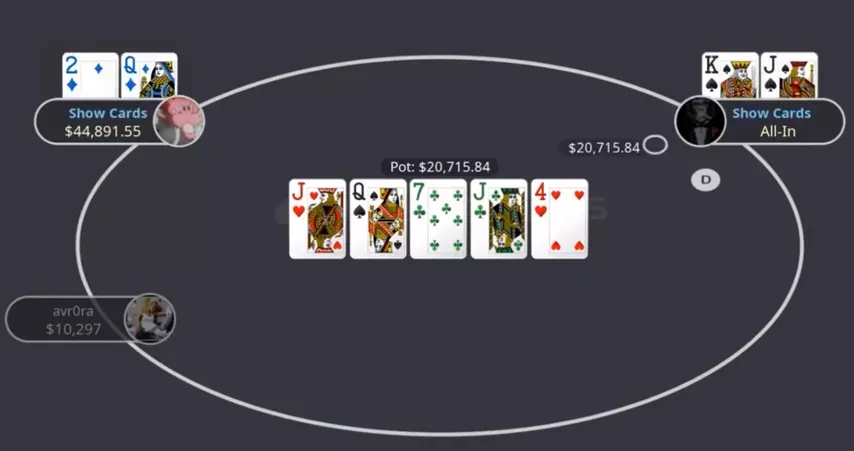
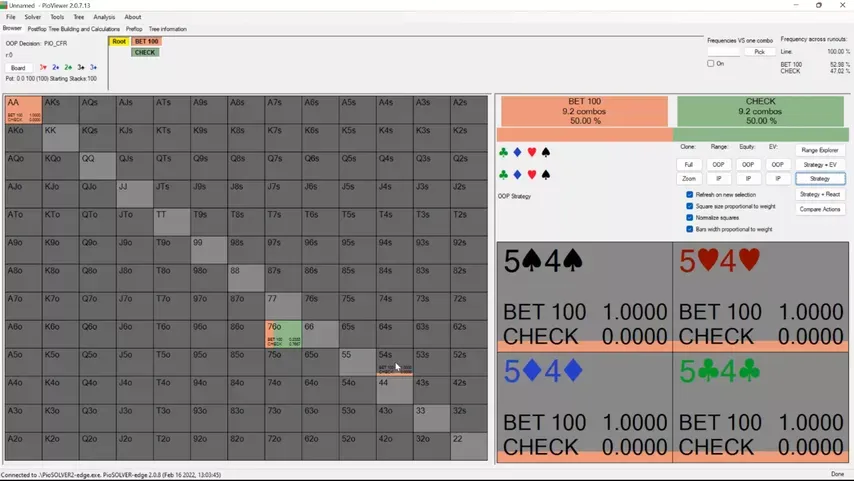
Let’s see how LLinusLLove, one of the best players in the world, deals with this situation. After defending the big blind with , Linus check-calls the flop with top pair.

The turn is a , and Linus leads, only to face a raise from Stefan.

The river is a complete blank, and Linus gets put to the test for the rest of his opponent's stack.

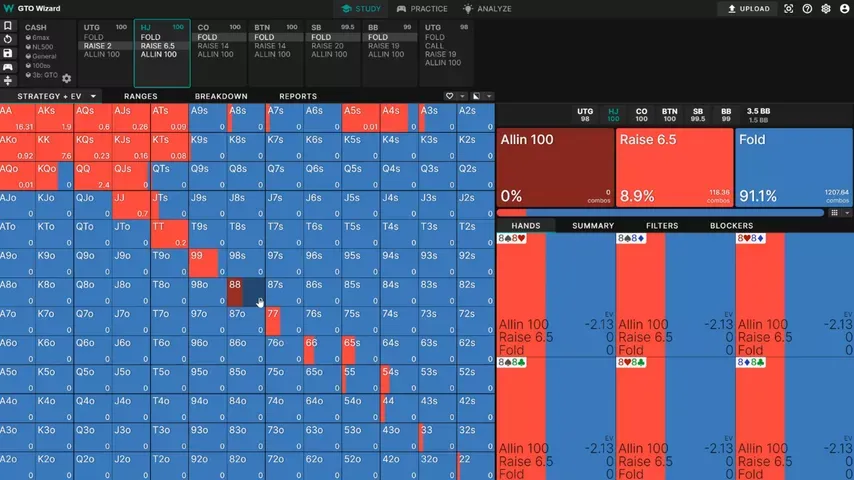
At first, looks like a really clear fold because we have so many better Queens to call with. But in this specific situation, our kicker doesn’t matter as much as you might think.
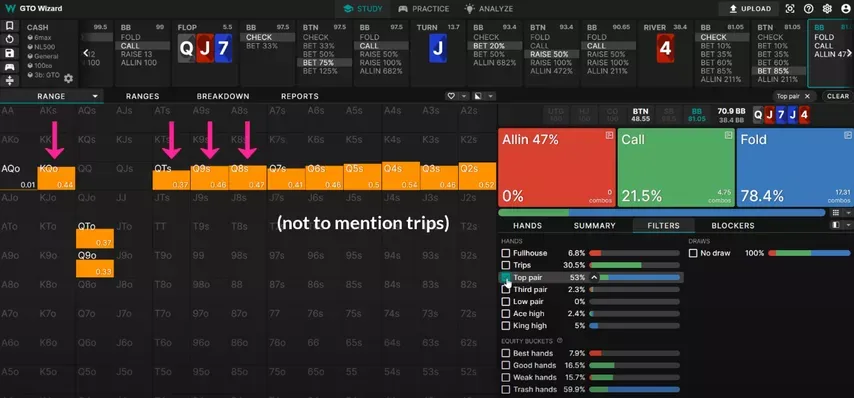
Given the turn raise and river jam, BTN’s range is extremely polarized. It wouldn’t make sense for him to do this with a , so in relative terms, and are really the same hand. also has the added advantage of unblocking most of BTN’s bluffs.
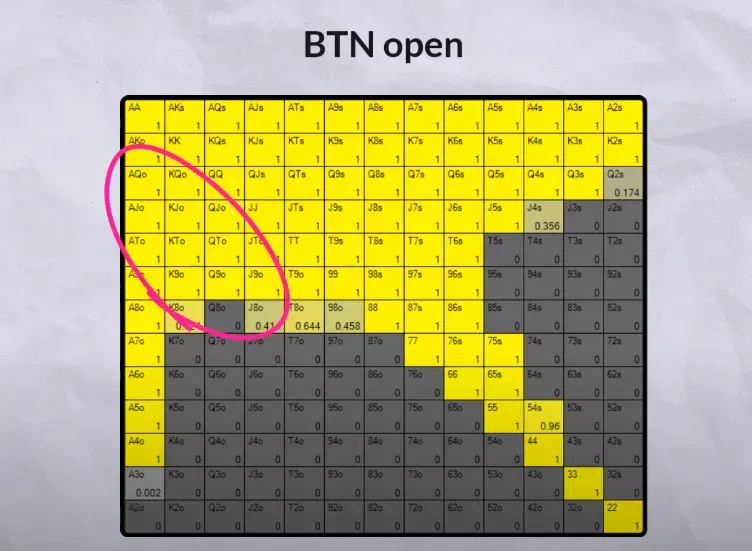
If you look at BTN’s opening range, it’s very weighted towards high offsuit cards. This naturally carries over to later streets, making low cards—such as the —especially good to bluff-catch with.
Therefore, it is more profitable to catch bluffs when we have a small kicker that does not block anything, since the probability that the opponent is bluffing increases. Because of this, a solver prefers to call a push with weak queens:
By having a kicker that doesn’t interfere with his high card region, we increase the probability that BTN is bluffing, making our call that much more profitable.
Looking at the solver solution, we see a clear preference for calling with lower kickers. BTN is bluffing with lots of hands like and , so we definitely want to avoid having a or .
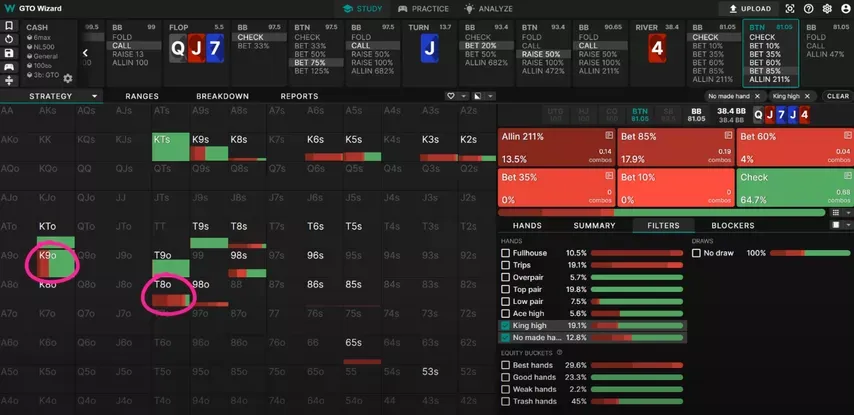
And while he is bluffing with the occasional and , these hands make up a much smaller part of his bluffing range since he doesn’t have the offsuit versions of them.
All in all, holding a has the effect of weighting BTN towards bluffs, which is why the solver calls at a higher frequency than .
But wait a minute, you might say. If having a is so good, wouldn’t having be even better? Well, as tempting as it might be to call down with Deuces 100% of the time, the fact is that we will always prefer to have a pair to the board. and are both hands with excellent unblockers, but the difference is that also blocks some value on top of unblocking bluffs. You can think of the as a card with neutral blocking effects—which is to say it blocks neither bluff nor value—and the as a card with positive blocking effects.
So the only time we call down with hands like is when we are already calling all of our one pair to the board and still need more hands to hit our target frequency—something that mostly happens when facing a small river bet. Conversely, when we are facing extremely large bets, the percentage of our range that we need to defend is much lower. Against a 2x pot-sized bet, for example, even is folding all the time. We can easily hit our target frequency by calling alone, and there is no reason to call over when the latter blocks so much more of BTN’s value range.

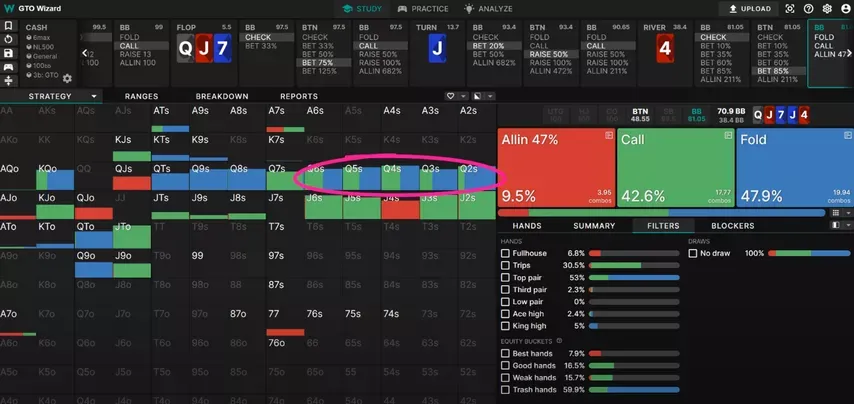
As for which combos of are better to call, you can probably already guess that the solver prefers defending the lower kickers over the higher ones.
If you’re following so far, you might be thinking to yourself: if the solver prefers to call down with hands that contain a 2, wouldn’t that make the 2 a great card to bluff with as well? And you would be absolutely right. Looking at BTN’s strategy, hands with a 2 or a 3 tend to bluff much more often compared to higher combos—not a surprise given that they block BB’s best calls.

But here’s where it starts to get confusing: if BTN is bluffing with so much , why does BB still prefer to call hands with a ? Wouldn’t it now be better to call with the higher kickers instead?
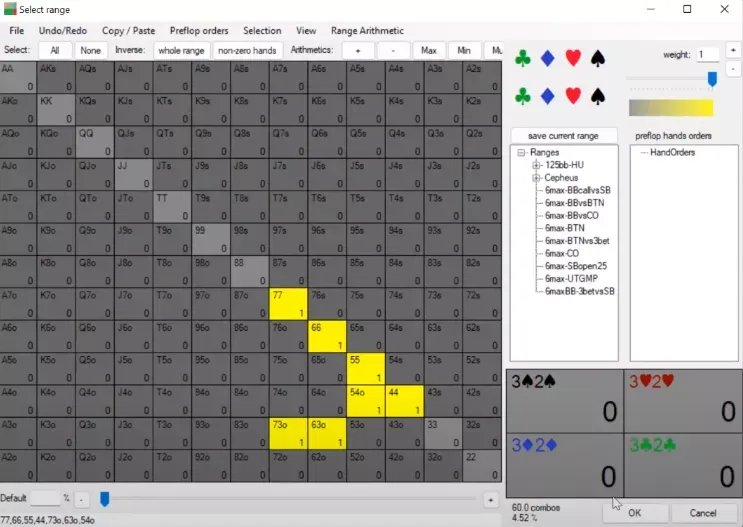
To understand this, let’s take a look at a simple toy game (The board is: ).
Here, OOP is the aggressor, with a range of and some bluffs.

In position's range consists of – , which are all pure bluff-catchers.
Notice how OOP selects his bluffs: suited—which he only has a tiny amount of—is bluffing all the time, while offsuit is giving up at high frequency.

This is happening because IP is calling and more often than and , making more valuable in terms of blockers.
At the same time, OOP bluffing with doesn’t discourage IP from calling with and because OOP’s bluffing range still contains way more than .
The point is that bluffing a certain hand at high frequency doesn’t necessarily mean the hand will be a big part of your bluffing range. This is why the is such a powerful card for both aggressor and defender: combos are scarce enough that the aggressor can bluff them all the time without discouraging the defender from calling down with bluff-catchers that contain a .
Remember: scarcity is king! Just like in real life, where scarce items are worth more, bluffs that are scarce also tend to have higher EV.
Here’s another example that illustrates the same concept. (The board is: ).
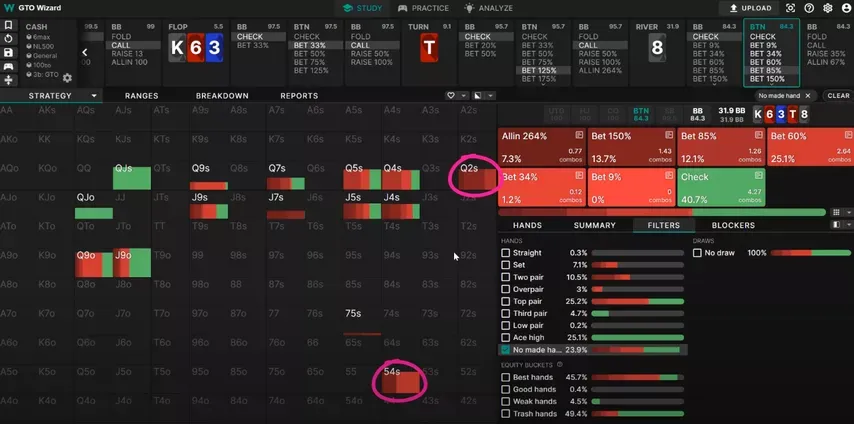
In this triple barrel line, BTN is bluffing all the time with hands like and . These low suited combos make up a relatively small part of BTN’s overall range, so even if he bluffs them all the time, BB cannot exploit him by preferring to bluff-catch with higher cards. Indeed, out of all BB’s hands, it’s the humble that is calling at the highest frequency.
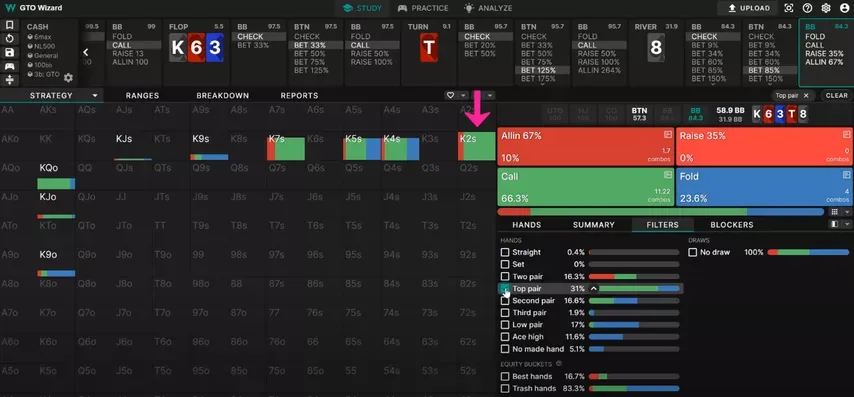
What if the button bluffed offsuit a lot instead of suited? Then the BB player would call with or and fold and . And once he adjusted, the button would lose money on bluffing with . And that's why the solver won't use those suited – because it's exploitable, and therefore contrary to GTO.
In short, scarce bluffs are gold in the solver world.
Now consider what happens if BTN were to bluff with the higher offsuit combos instead. BB would have a really easy counterstrategy of calling with lower kickers and folding the ones with higher kickers. And once that happens, it would be a big mistake for BTN to bluff with hands like . For this reason, bluffing with cannot be GTO.
Scarcity sounds like a simple enough concept to implement, but you might be thinking to yourself: surely there’s more to blockers than this? Whatever happened to choosing bluffs that block villain’s nut hands and unblock his missed draws?
To give you some idea of the relative importance of these factors, let’s make a few changes to our toy game. Let’s add a bunch of and to in-position's range to represent nut hands that are always calling.
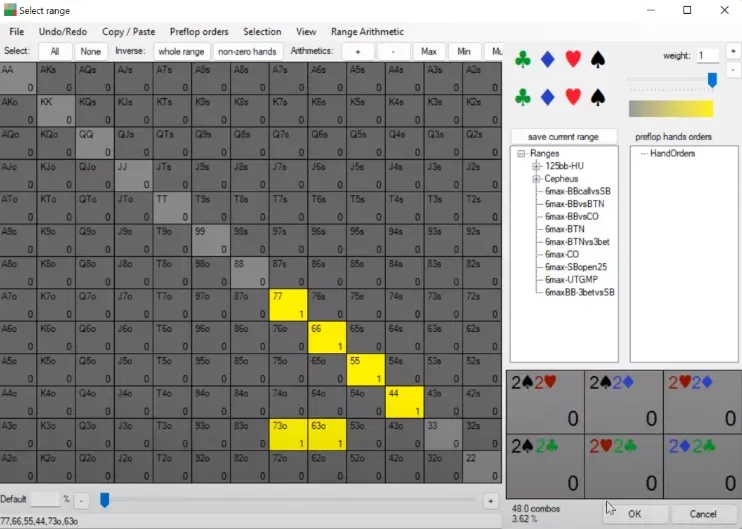
You might think that this would make a better hand to bluff with since we block IP’s highest EV calls...
... but when we rerun the sim, we see that the solver still prefers to bluff with .
Next, let’s add a bunch of to IP’s range, to represent missed draws that are always folding to a bet.
Again, upon resolving, we see that this has very little effect on OOP’s strategy.
Despite blocking a chunk of missed draws and not blocking any nut hands, is still bluffing all the time. It’s a shocking result, because these things are exactly what most players will look out for when choosing bluffs. And yet, in this example at least, scarcity is by far the dominant factor.
What this goes to show is that you can’t really go wrong with bluffing scarce hands on the river. Regardless of what else you block or unblock, will be at least 0EV to bluff in most situations, and outright profitable in many others.
- Increased first deposit bonus
- Increased rakeback and reloads
- Help with deposits and cashouts
- Access to private freerolls
- Round-the-clock support
Another interesting property of hands that contain a is that they often have better implied odds. Take a look at UTG’s response vs a 3-bet:
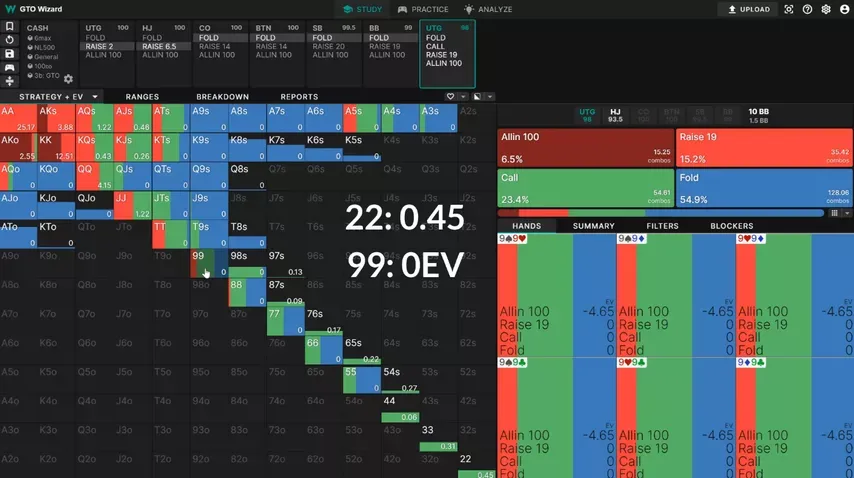
is a slightly higher EV call than , despite being a much weaker hand. Part of the reason is that IP is not 3betting – very often, nor does he have much and below.
So actually isn’t that far off from in terms of raw equity. For the most part, we are either crushed by a bigger pair, or flipping against a hand with overcards. On top of that, the times we flop a set, is likely to win more money than . This is because the board tends to be much more disconnected with a on it.
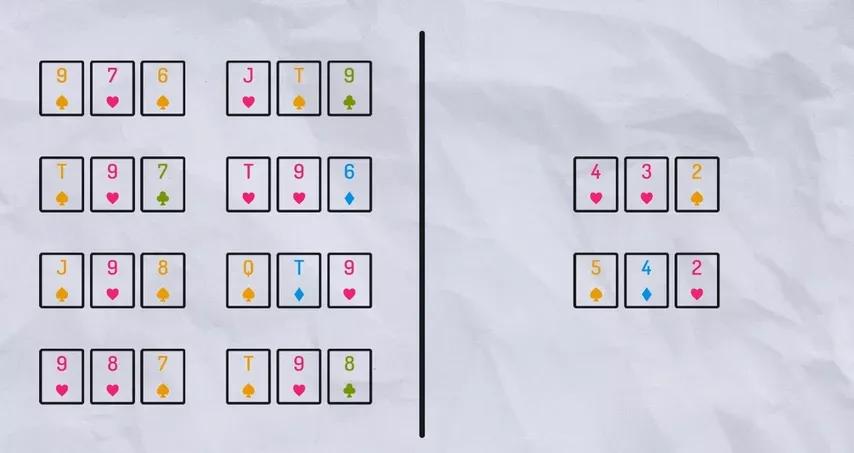
Here’s a simple experiment: how many connected boards can you think of that contain a ? How many can you think of that contain a ?
The more coordinated the board is, the less inclined the aggressor will be to stack off with his overpairs. So even if we do get lucky and hit a set of nines, the pot tends to be much smaller on average. Whereas if we spike a set of deuces, there is a much higher chance that our opponent will pay us off, since the board isn’t likely to be as scary-looking.
Putting two and two together, this makes a slightly more profitable hand to defend vs the 3bet, since it has similar EV the times it doesn’t hit a set, and better EV the times that it does.
What we’ve seen in this video is that the 2 is a much more relevant card than most players think.
In particular, the scarcity of 2x combos means that they will more often than not make good bluffing candidates.

There is 1 more important concept to know here, and I discuss it in a webinar for GTO Wizard. I also go into more detail about why blocking nut hands or unblocking missed draws isn’t as important as you might think.